One of the most common questions people have about YubiKeys, and security keys in general, is: “What if I lose my key?”
While WebAuthn and FIDO2, the open standards for security key authentication, promise strong, phishing-resistant and — perhaps most importantly — easy-to-use multi-factor authentication, this question still remains. As of today, there are no answers that offer an excellent user experience without making compromises on security.
Yubico’s mission is to make the best security easy to use, which often means developing new technologies to solve big problems. In this blog, we’ll take a closer look at Yubico’s recent proposal to the World Wide Web Consortium (W3C) to add a user-friendly solution for backup security keys to the WebAuthn standard. We’ll also discuss our collaboration with researchers at the Surrey Center for Cyber Security to develop a new cryptographic building block for it.
Background
First, let’s talk about the current state of affairs. The standard answer to the opening question in this blog, “What if I lose my security key?”, is that you enroll two keys with every service or application you’re protecting. By doing this, you prepare a backup security key in advance, much like you have a spare key to your house, your office, or your car. However, the user experience with this approach is not ideal.
If you store the backup security key away — say, in a drawer at home, or a bank deposit box — you would need to retrieve it every time you register with a new service. Not only is this inconvenient, but the additional handling also increases the risk that you lose the backup key, which would defeat the very purpose of it.
A few solutions have been proposed, but they all come with additional trade offs or concerns:
- Some rely on sharing private key material, which is not only generally frowned upon, but also causes issues with authenticator attestation and signature counters.
- Some rely on generating a lot of key pairs in advance and sharing the public keys, which isn’t feasible for devices with limited storage capacity like security keys.
- Some rely on backing up keys to a third-party service, which certainly can be done but introduces a new dependency on the availability of that third-party service.
- And finally, some approaches only work for U2F-style keys stored on the server, and some only work for discoverable keys stored onboard the security key.
In short, we were not completely satisfied with any of the solutions proposed thus far, which is why we chose to develop our own. We believe our proposed solution strikes a better balance between security and usability.
Yubico’s proposal
If we were to imagine a perfect solution, we would like one where we can set up a backup security key once and not have to think about it until we lose the primary security key. At that point, we would retrieve the backup security key and it would “just work”. Ideally, all of the services we’ve already registered our primary security key with would also automatically know we’ve moved to the backup security key, and revoke access for the lost key.
Fortunately, Yubico’s proposed solution gets most of the way to the scenario described above. Using the YubiKey as an example, our solution would work like this:
1. First, you get two YubiKeys and use a software tool (such as YubiKey Manager in the context of YubiKeys) to associate the two devices with one another, making one the “backup” YubiKey and the other the “primary” YubiKey.
2. You can now store the backup YubiKey away somewhere safe, and use the primary YubiKey as usual. The next time you log in with the primary YubiKey, the website will also detect that you’ve set up a new backup YubiKey and ask you to register it by simply tapping the gold disc on the primary YubiKey. The same goes whenever you register with a new site for the first time.
3. Now, if you lose the primary YubiKey, you start logging in by providing your username and password as usual. When prompted for your YubiKey, you instead select “I lost my security key”. This will instead prompt you for your backup YubiKey, which you retrieve from where you stored it.
4. The service verifies the backup YubiKey and grants access. At the same time it automatically revokes access for your lost YubiKey, “promotes” the backup YubiKey as the new primary key, and sends you an email notification about these changes to your account.
5. You can now get a new YubiKey and set that up as your new backup by going back to step one.
Unfortunately, there’s still no way to perform the recovery procedure for all services at once, but at least this solution minimizes the manual effort needed to set up and maintain backup security keys.
How it works
So, how does this all work under the hood?
In our proposal, the initial setup to associate the two security keys with one another creates a cryptographic link between the two security keys, allowing the primary security key to generate public keys on behalf of the backup key. However, the primary security key does this without knowing the corresponding private keys, and like all WebAuthn public keys, these public keys are non-correlatable to prevent tracking users between services.
Along with the backup public key, the primary security key registers a “key handle” for it. The first time you log in with the backup security key, the service sends it the key handle, which the backup security key uses to derive the backup private key. At the same time, the backup security key also generates a new public-private key pair to replace the backup key pair that was generated initially. From then on, you can log in as you normally would.
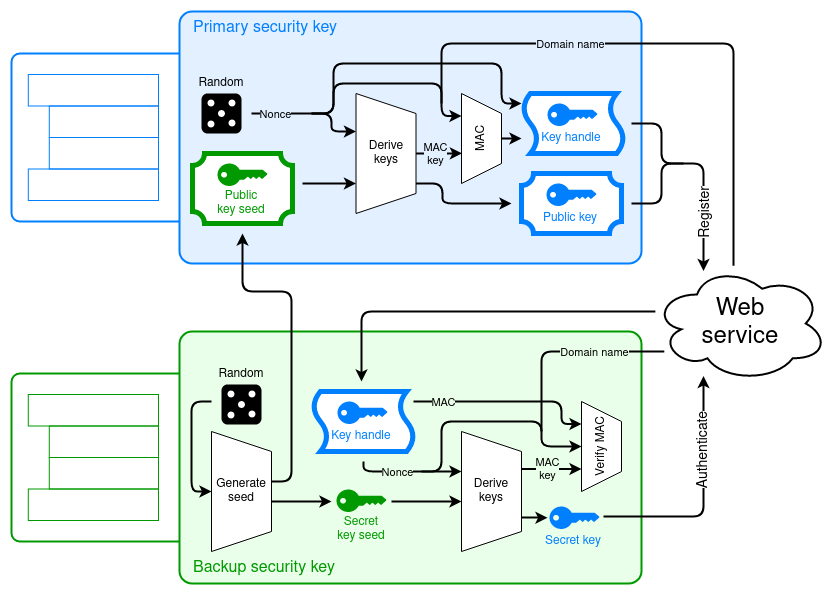
This cryptographic link enables backup key pairs to work much like U2F key pairs do: the private keys are actually stored on the relying party’s server instead of on either security key. But even so, only the backup security key can access the private keys. This means that backup key pairs don’t consume storage space on either security key, so you can have backup key pairs for an unlimited number of services.
It also doesn’t matter whether the primary key pair is a discoverable key that is stored on the primary security key, or a U2F-style key pair that is stored on the relying party’s server. Since the backup key pairs are their own separate key pairs, they can be used for both.
Securing cryptographic proof
Last year, Yubico teamed up with a group of researchers at the Surrey Centre for Cyber Security to help prove the security of the cryptographic operations in our proposed WebAuthn protocol. This work was presented at the ACM CCS conference on November 11, 2020.
The research team, consisting of Dr. Mark Manulis, Nick Frymann, and Daniel Gardham, has not only proved the security of Yubico’s proposal, but also generalized it. They model our protocol as an instance of a new abstract functionality called “Asynchronous Remote Key Generation” (ARKG), and prove that any instance of ARKG can be composed with any public key protocol. This makes ARKG an interesting construct in its own right and also paves the way for new instantiations, possibly using other cryptographic techniques beyond elliptic curves.
Looking forward
With the cryptographic security proof in place, we’re confident that this work can form a solid basis for a much needed backup solution for WebAuthn security keys. To that end, we’ve proposed our solution to the W3C Web Authentication Working Group as an official protocol extension, but a lot of standardization work remains to be done.
The solution will also require services to implement support for it, which will take considerable work, but can be aided by reusable software libraries. Either way, Yubico remains committed to making the best security easy to use for everyone.
Read Yubico’s full implementation proposal here, and the research paper here. The full ACM CCS conference presentation can also be viewed here.
We are very grateful to Dr. Manulis, Mr. Frymann, and Mr. Gardham for helping us push the state of the art forward!
—
Appendix: Diving into the math
Our proposal makes use of the simple relationship between private and public keys in elliptic-curve cryptography, and uses a small arithmetic trick to “mask” a private key by combining a randomly generated public key with a designated “seed” public key.
In elliptic curve cryptography, a private key is simply an integer p and the corresponding public key P = p * G is p times the generator element G for the curve group. In the initial setup, the backup security key creates a “seed” key pair (s, S) and transfers the public key S to the primary security key. To generate a backup public key, the primary security key performs an ephemeral elliptic curve Diffie-Hellman (ECDHE) key exchange with the seed public key S: it generates a random key pair (e, E) and computes e * S. It uses HKDF to expand e * S into an integer c and a HMAC key m, and computes a backup public key P = c * G + S. Finally, it computes a HMAC signature over E, P and the server’s web address, and returns E, P and the HMAC signature to the server.
The backup security key can derive the corresponding public key p using E as follows. First, the server sends E and the HMAC signature to the backup security key. Since the backup security key has the seed private key s, it can compute s * E = s * e * G = e * S and thus compute the same c and m as before. Now it can verify the HMAC signature, to make sure the backup key is valid for this server and this security key, and compute the private key p = c + s. p forms a valid key pair with P since P = p * G = (c + s) * G = c * G + S. This private key p can now be used to create an authentication signature, and the server can accept it since it already trusts the public key P.
This is actually not a wholly new idea – it’s also been proposed as the basis of the Dual-Key Stealth Address Protocol for blockchains. However, until now we weren’t able to find a cryptographic proof that the raw elliptic curve operations are secure. Thanks to Dr. Manulis and his team’s work on ARKG, we are confident that our proposal meets the highest security standards and is suitable for use with WebAuthn.





