In Part 1 of our crypto blog, I briefly introduced the concept of asymmetric encryption algorithms and the general rule that the longer the key the better. Let’s take a deeper look at that logic here in Part 2.
There are many asymmetric encryption algorithms, but lets focus on RSA, which is one of the most popular and is supported by YubiKey NEO and NEO-n. What is a suitable key length to use with RSA and why not just use the longest key possible?
RSA was first introduced in the ‘70s but since it is based on a mathematically hard problem as discussed in Part 1, we are still able to use it with some adaptations.
Historically, a common starting point for a key length has been 1024 bits. Despite the fact that attacks on this key length are very sophisticated and targeted to specific platforms, 1024-bit keys are generally considered not secure enough and their use is highly discouraged.
In 2012, the National Institute of Standards and Technology (NIST), a U.S. agency that promotes technological advancements, published this document, which contains the following table (Table 4 on page 67).
| Security Strength | 2011 – 2013 | 2014 – 2030 | 2031 – beyond | |
| 80 | Applying | Deprecated | Disallowed | |
| Processing | Legacy use | |||
| 112 | Applying | Acceptable | Acceptable | Disallowed |
| Processing | Legacy use | |||
| 128 | Applying/ Processing | Acceptable | Acceptable | Acceptable |
| 192 | Acceptable | Acceptable | Acceptable | |
| 256 | Acceptable | Acceptable | Acceptable | |
The column “Security Strength”, or more colloquially “Bits of Security” is an estimation of the amount of work required to defeat a cryptographic algorithm, and therefore the higher the value, the better.
The keywords “Applying” and “Processing” refer to encryption and decryption operations respectively.
A Security Strength of 80 bits is currently “Disallowed” which translates to “an algorithm or key length [that] shall not be used for applying cryptographic protection.” Now, if you were guessing that 80 bits of security are approximately equivalent to RSA-1024, you have guessed right. This is mentioned in the same NIST document (Table 2, page 64).
Similar results can also be found in a yearly report (Tables 7.2 and 7.3 on page 30) from ECRYPT II, the second incarnation of ECRYPT, the European Network of Excellence in Cryptography. For clarity, in the following text we will use the data from the NIST publication.
The next relevant value in the table is 112 bits of security, which roughly corresponds to RSA with a key length of 2048 bits. At the moment this value is considered “Acceptable,” which means that it is not known to be insecure and it is deemed to be so until 2030.
Now comes the interesting bit. Although there is no requirement to use RSA keys with a length that is a power of two, depending on the implementation there might be some advantages in terms of speed.
For this reason we take into account a length of 4096. Unfortunately, this value is not on the table above. However, with a bit of exponential regression and assuming that the “Security Strength” function is continuous (or better, derivable) between the data points provided in the table above, we get the following plot: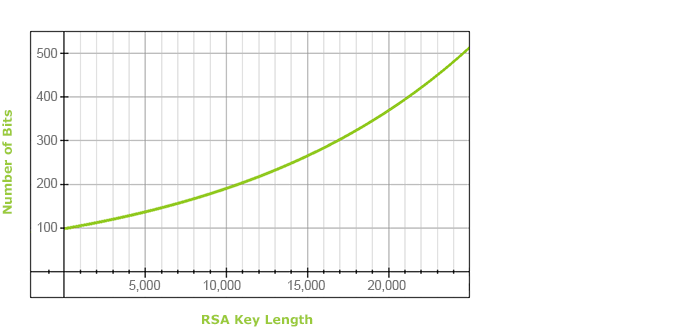
As you can see, a 4096-bit RSA key clocks in at around 129 bits of security.
This value is marginally better than a key length of 3072 bits, and considered acceptable beyond year 2030. (Also see this key length calculator).